
 |
Articles |  |
| Home | Articles | Presentations | Downloads | Politics | Fun |
 |
|
|||||||||||||
מהו מחשב קוונטי?מאת שחר דולבפורסם ב'גלילאו' 77, ינואר 2005.
מהו מחשב?בכדי להבין מהו מחשב קוונטי, אסקור תחילה מהו מחשב 'קלאסי'[1]. מהי מכונת טיורינג?מכונת טיורינג היא הפשטה של המחשב הדיגיטלי. היא סוג של מחשב שקשר שלו לעולם מתבצע באמצעות סרט עליו כתוב הקלט, ועליו נכתב הפלט. הסרט מחולק לתאים, בכל תא כתוב סימן בודד - מספיק להשתמש בסימנים 0 ו-1. למחשב ראש קורא/כותב שנמצא בכל רגע נתון מעל אחד התאים שבסרט. למכונה 'תוכנה' הבנויה מטבלה של 'מצבים' כל שורה מהווה מצב. בכל רגע נתון המכונה נמצאת באחד המצבים. פעולתה מתמצת בקריאת הסימן שנמצא מתחת לראש, ופעולה בהתאם לכתוב בטבלה. בטבלה ישנן ההוראות הבאות: אם נמצא הסימן 0 על המכונה לכתוב במקומו סימן כלשהו (0 או 1), לאחר מכן לנוע ימינה או שמאלה, ולבסוף לעבור למצב חדש. וכן אם נמצא הסימן 1, מה לכתוב, לאן לנוע ולאיזה מצב לעבור. למכונה תא זיכרון בודד ובו מספר אחד: המצב בו נמצאת המכונה. מתחילים ממצב 0 ומתחילים לבצע את ה'תכנית': המכונה קוראת את המספר שמתחת לראש ומתחילה לפעול בהתאם ל'תכנית'. הפעילות מסתיימת כשהמכונה מקבלת הוראת 'עצור'. 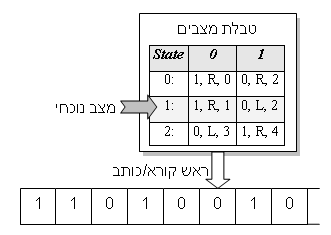
ובכן, מהו מחשב? התשובה הפשוטה היא: "אותה קופסה שיש לחלקנו על שולחן העבודה, הגורמת לרגשות תסכול וזעם כה רבים". אבל הרי יש צורות רבות למחשב - מחשבוניית חרוזים, דרך שעון דיגיטלי, ה'מוח' האלקטרומכני השולט על מכונת הכביסה, ועד לאותן קופסאות המכונות מחשבים אישיים. מה המשותף לכל היחידות הללו, והאם ניתן לבנות מודל תיאורטי שיתאר את כולן? השאלה הזו עלתה בראשית המאה העשרים, עוד בטרם יוצר המחשב הדיגיטלי הראשון, כשאלה מתמטית תיאורטית. בשנת 1936 הצליח המתימטיקאי אלן טיורינג ליצור לראשונה מודל למכונת חישוב אוניברסלית – מודל שיוכל לבצע חישובים שונים, בהתאם לתוכנה שהוזנה לו. המודל נקרא 'מכונת טיורינג' והוא מתאר מכונת חישוב בסיסית ביותר. מאז מקובלת ההנחה, הניקראת "תיזת צ'רץ'-טיורינג", הטוענת כי כל רעיון חישובי שיכול לעלות על דעתנו ניתן לתיאור על ידי מכונת טיורינג. אם תיזה זו נכונה, הרי שכל המחשבים שווים - כל חישוב שנעשה על מחשב כלשהו ניתן לתיאור על ידי מכונת טיורינג מתאימה. ההנחה הרווחת כיום היא שהתיזה נכונה, למרות שאין הוכחה פורמלית לכך. ומה עושה מכונה זו (ובעצם, כל מחשב)? מקבלת אוסף נתונים כקלט, ומחזירה אוסף נתונים אחר - פלט. המחשבים שאנו נדון בהם הם 'דיגיטליים', דהיינו 'סיפרתיים'. משמעות הדבר היא שכל נתון מקודד למספר (digit), והמחשב יודע לבצע מניפולציות על מספרים. כך, למשל, מעבד תמלילים ממיר כל תו למספר ('א'=224, 'ב'=225, וכו') וכך הוא יכול להתמודד עם הטקסט המוקלד. מערכת ההפעלה יודעת להפוך כל מספר שכזה, המייצג אות אחת, ולהמירו לתבנית של נקודות שחורות ולבנות (המיוצגות על ידי הספרות 0 ו-1) לצורך ההצגה על המסך, וכו'. בעולם המחשבים כל מספר מקודד בשיטה הבינארית, בעזרת שתי הספרות 0 ו-1 ('ביט'), כך שכל תהליך חישוב מתחיל מאוסף של ספרות בינאריות ('ביטים') כקלט, ומחשב אוסף של ספרות בינאריות כפלט. אוסף הפעולות שהמחשב מבצע ניקרא 'אלגוריתם'. לדוגמה, אלגוריתם הבודק אם מספר נתון X הוא ראשוני (מתחלק ללא שארית רק בעצמו וב-1) יכול להיראות כך:
מהו קוד בינארי?באופן יומיומי אנחנו משתמשים בשיטת ספירה על בסיס 10. לשם כך אנו משתמשים בעשר ספרות: 0, 1, .., 9, ובמבט מימין לשמאל, כל סיפרה מייצגת ערך הגבוה פי עשר מהספרה לידה. הקוד הבינארי מתבסס על שיטת ספירה בבסיס 2. לשם כך יש להשתמש אך ורק בשתי ספרות: 0 ו-1, כאשר במבט מימין לשמאל, כל סיפרה מייצגת ערך הגבוה פי 2 מזו שלידה: 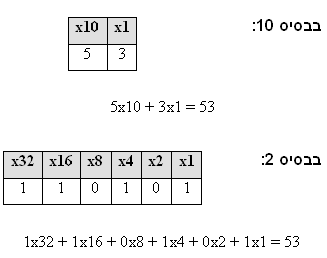
זהו אלגוריתם המקבל מספר אחד כקלט (X) ומפיק מספר אחד הפלט (0: X אינו ראשוני, 1: X ראשוני). כדי שאפשר יהיה להורות למחשב לבצע אלגוריתם זה יש לכתבו באופן פרטני באחת משפות התכנות ולהזינו למחשב. יש לשים לב לעובדה המעניינת, שבהזיננו את האלגוריתם למחשב, אנו הופכים גם אותו לקלט, זאת-אומרת, לאוסף מספרים שניתנים לעיבוד במחשב. תורת הסיבוכיותאולם, מסתבר שלא כל החישובים נולדו שווים. עוד בימים בהם מחשב אלקטרוני היה בגודל של חדר וכוח המחשוב שלו היה שווה בערך לכזה של שעון דיגיטלי ממוצע בימינו, כבר ידעו המתמטיקאים כי יש חישובים מסוימים שהם 'קשים מאד' לביצוע, ואחרים כלל אינם אפשריים. חישוב מסוים שאינו ניתן לביצוע על ידי אלגוריתם הוא השאלה הבאה, הנקראת 'בעיית העצירה': "בהינתן אלגוריתם וקלט מסוימים, האם חישוב האלגוריתם על הקלט יפסק אי פעם?" כולנו מכירים את המצב המתסכל בו המחשב 'נתקע' - אינו מגיב לעכבר או למקלדת ויש ללחוץ על כפתור האיתחול (Reset). במצב זה התוכנה שאנו מריצים נקלעה לחישוב ארוך, שיכול להיות שלא יסתיים לעולם. וזו הדילמה: אם אאתחל המחשב עכשיו אאבד את כל המידע שעדין לא שמרתי, אולי בעוד רגע המחשב 'יתעורר' ואוכל להמשיך לעבוד, מאידך, המחשב יכול להישאר תקוע לעולם ועד. אם שאלתם את עצמכם מדוע מהנדסי התוכנה לא מצאו את כל קיטעי הקוד הסוררים וסילקו אותם מבעוד מועד, התשובה פשוטה: ניתן להוכיח כי אין שום תהליך אלגוריתמי שיכול להכריע אם תכנית מסוימת (מיקרוסופט וורד, למשל) תרוץ לעולמי עד או תיעצר מתישהו.[2] כמובן שעבור תהליכים פשוטים (כמו, למשל, האלגוריתם שנתתי לעיל לבדיקה אם X ראשוני) ניתן לבדוק ולאשר שהם יעצרו עבור כל קלט (מה יקרה אם האלגוריתם שנתתי יקבל את המספר מינוס אחת כקלט?). אך אין אפשרות לבדוק כל תכנית על כל קלט אפשרי. משפחה אחרת של בעיות היא של בעיות קשות מאד לחישוב. 'קשות' במובן שהן לא ניתנות לחישוב עבור קלט מורכב. בעיה קלאסית ממשפחה זו היא בעיית הסוכן הנוסע: לסוכן ניתנת מפה עם מספר ערים והוא חייב לבקר בכולן. כיצד עליו לנסוע בכדי לבקר בכל הערים, כך שאורך המסלול יהיה הקצר ביותר? מסתבר שעליו לבדוק את כל המסלולים האפשריים ולבחור מביניהם את הקצר ביותר - אין שיטת חישוב יעילה יותר. עבור 5 ערים יש 120 מסלולים אפשריים, עבור 10 ערים: 3 מיליון, עבור 15 ערים: 1,307,674,368,000! זו אינה שאלה תיאורטית לחלוטין, אם מהנדסי אינטל רוצים לחשב כיצד לחווט באופן אופטימלי את כל 55 מיליון הטרנזיסטורים שעל מעבד הפנטיום 4, הם צריכים לבצע חישוב דומה. גם אם ישתמשו בכל אטום ביקום כתא זיכרון במחשב אינטר-גלאקטי, ואם היו מחשבים מיום לידת היקום ועד היום, לא היה מספיק הזמן לסיום החישוב... באופן עקרוני, בעיה נחשבת ל'קשה' לפיתרון אם עבור קלט בגודל N (למשל, מספר הערים שעל הסוכן הנוסע לבקר) יש לבצע סדר גודל של N2 חישובים. שערים לוגיים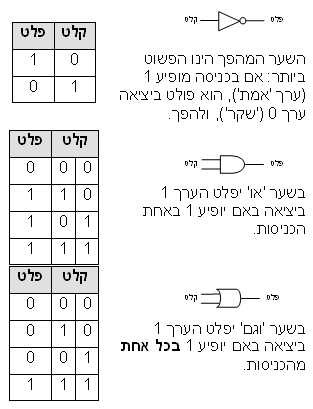
תרשים 1לאחר שמדעני המחשב למדו כל זאת, נשאלה השאלה האם טכנולוגיית מחשוב שונה תאפשר להתגבר על מכשלות אלו. הרעיון הראשון היה לחשב במספר מחשבים באופן מקבילי. כך, אם ניתן לחלק את הבעיה באופן מיטבי (ולא כל בעיה ניתנת לחלוקה שכזו), ביצוע מקבילי על שני מחשבים יקצר את זמן החישוב פי שתיים, עשרה מחשבים - פי עשר, וכן הלאה. אך כפי שאמרנו, עבור בעיה קשה יש לבצע N2 חישובים, זאת אומרת שקיצור התהליך פי שתיים יאפשר הגדלת הקלט בעוד יחידה אחת בלבד (להוסיף עוד עיר אחת, לדוגמה), וקיצור זמן החישוב פי 100 יאפשר הגדלת הקלט בפחות משבע יחידות (27=128) ... בהמשך ניראה כי מחשב קוונטי מאפשר מקביליות מסדר הגודל של N2, זאת אומרת שבעזרת מחשב קוונטי כן ניתן יהיה לחשב בעיות 'קשות'. אך בעיות בלתי ניתנות לחישוב (כגון 'בעיית העצירה') לא ניתנות לפיתרון גם בעזרת המקביליות העצומה של המחשבים הקוונטיים. מעגל אוניברסליבטרם נפנה למחשב הקוונטי נבחן עוד היבט אחד של המחשבים הקלאסיים: נוח לתאר מחשב באופן אחר, השקול לחלוטין למכונת טיורינג, זה הוא ה'מעגל הבוליאני'. 'בולאני' על שם ג'ורג' בול, מתמטיקאי בן המאה ה-19 שניסח באופן מודרני את חוקי הלוגיקה ('לוגיקה בוליאנית'). במעגל בוליאני מתוארות הפעולות הלוגיות ההופכות את הקלט לפלט. מסתבר שניתן לתאר כל מחשב באמצעות שלוש פעולות לוגיות בסיסיות. פעולות אלו נקראות 'שערים לוגיים' והן: שער 'מהפך' (NOT, או 'לא'), שער 'או' (OR), ושער 'וגם' (AND) (ראו תרשים 1). לתיאור הפעולות הלוגיות שמבצע מחשב יש לחבר שערים שונים. למשל, פעולת חיסור בינארית היא פשוטה ביותר: 1-1=0, 1-0=0, 0-0=0 ו-0-1=1-, לצורך העניין נסמן 0-1=1. ניתן לראות בתרשים כיצד יש לחבר את השערים הלוגיים כדי לקבל מעגל מחסר (תרשים 2). מעגל 'מחסר'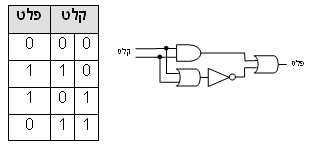
תרשים 2האמת היא שניתן לייצר את שלושת השערים היסודיים על ידי חיבורים שונים של מספר שערים מסוג אחד הנקרא 'לא-וגם' (NAND), אני אותיר לקוראים למצוא כיצד ניתן לחבר שערי NAND לקבלת כל אחד משלושת השערים שהוזכרו לעיל. השער NAND ניקרא שער אוניברסלי היות ובעזרתו ניתן להרכיב כל פעולת חישוב אפשרית. בינתיים, בעולם הקוונטי...אחד ההבדלים המהותיים בין העולם הקוונטי לעולם הקלאסי המוכר לנו מחיי היום-יום הוא שבעולם הקוונטי עצמים יכולים להיות במצב של 'סופרפוזיציה'. סופרפוזיציה נובעת מהעובדה שברמה הקוונטית, חלקיקי החומר מתנהגים כגלים. ניתן להרכיב שני גלים, המתארים את החלקיק בשני מצבים שונים, זה על זה. כך מתקבל גל אחד שמבחינה מסוימת הוא גם בשני המצבים בו זמנית, אך בעצם אינו באף אחת מהם (היות והוא שונה מכל אחד מהגלים בנפרד). שער 'לא-וגם'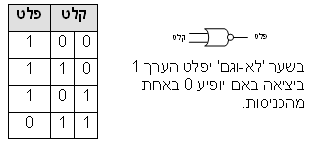
תרשים 3את המצב הקוונטי נהוג לסמן כך: <מצב|, כשבתוך סימן ה-< | ישנו ציון המצב. כך, למשל, מחשב קוונטי ישתמש בחלקיקים המסוגלים להיות בשני מצבים: 'אפס' <0|, ו'אחת' <1|. סימון כללי זה פוטר אותנו מהצורך לציין את פרטי הגל הקוונטי המתאר מצבים אלו, והוא יספיק בכדי לתאר את כל מוזרויות העולם הקוונטי. ובכן, המחשב הקוונטי ישתמש בחלקיק המהווה 'ביט' בודד. אך היות ועקרונות הסופרפוזיציה מאפשרים לחלקיק קוונטי להיות במצב שהוא הרכבה של שני מצבים שונים, יחידת המידע היסודית הקוונטית נקראת 'קיו-ביט' (qbit). כך, למשל, אפשר ליצור מצב בו החלקיק נמצא שליש במצב <0|, ושני שליש במצב <1|. על פי התורה הקוונטית, המקדם (נקרא גם ה'עוצמה') של המצב בריבוע מבטאת את ההסתברות למציאת המצב המסויים, כך שמצב 'שליש/שני-שליש' יראה כך:
במצב זה, אם נמדוד את החלקיק כדי לברר האם הוא במצב <0| או <1| נמצא בשליש מהמקרים את המצב <0| ובשני שליש מהמקרים את המצב <1|. אין שום אפשרות לדעת מראש מה תהיה התוצאה. יש לציין שמצב זה שונה באופן מהותי ממצב 'תערובת' שבו מערבבים חלקיקים ששלישם במצב <0| ושני שלישים במצב <1|. במצב שמתואר לעיל כל אחד מהחלקיקים נמצא במצב סופרפוזיציה. זו נקודה חשובה ביותר והיא תיבחן שוב בהמשך. הבעיה היא שלעולם לא נוכל למדוד את מצבו של חלקיק קוונטי ולקבל כתוצאה שהוא בשני מצבים בו בזמן. היות ובעולם המאקרוסקופי מצבי סופרפוזיציה לעולם לא ימצאו, אזי או שמכשיר המדידה יצביע על מצב א' או על מצב ב', אבל לעולם לא על שניהם. כך שבעצם אין אפשרות למדוד ממש את המצב הקוונטי, אלא רק באופן עקיף: נשתמש באוסף גדול מאד של חלקיקים במצב המתואר, נמדוד את כולם ונמצא ששליש במצב <0| ושני שליש במצב <1|. יש עוד לוודא שאנו לא במצב התערובת. התיאוריה הפיסיקלית מספקת לנו מדידות מסויימות שבעזרתן ניתן להבדיל בין מצב סופרפוזיציה למצב תערובת. במידה מסויימת ניתן לראות את המצב שתואר לעיל כ'סיבוב' ב-190של קיוביט ממצב <1|. נזכור שהמקדמים של מצבי ה-<0| וה-<1| בריבוע מהווים הסתברות, וזו חייבת להסתכם לאחת (ההסתברות למצוא או <0| או <1| היא 100%), וזה מזכיר את חוק פיתגורס: A2+B2=C2 במקרה שלנו:
כאשר 1/3 ו-2/3 הם צלעות של משולש ישר זוית, ו-1 הוא היתר. באופן גרפי ניתן לתאר את המצב המסובב כך: 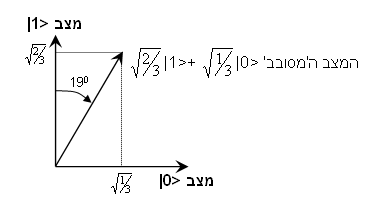
תרשים 4יש לציין שהמצב אינו ממש דומה לסיבוב כפי שאנו מכירים אותו היות והמקדמים של המצבים בסופרפוזיציה יכולים להיות גם מספרים מרוכבים (דהינו סכום של מספר 'רגיל' ושל המספר המכונה i, הלא הוא השורש הריבועי של 1-). מצב כזה יכול להתקבל, מהבחינה המתמטית, אם זווית הסיבוב בעצמה תהיה מספר מרוכב. מהו מחשב קוונטי?התשובה הקצרה היא: מחשב קוונטי הוא מחשב שבתאי הזיכרון שלו חלקיקים קוונטיים בודדים. אך לעובדה פשוטה זו יש השלכות נרחבות. כאמור, כל קיוביט יכול להיות במצב של סופרפוזיציה של <0| ושל <1|. במצב כזה, כל חישוב שיערך על הקיוביט יסתיים בסופרפוזיציה של תוצאת החישוב על <0| יחד עם תוצאת החישוב על <1|. היות והחישובים שניתן לבצע עם קיוביט אחד הם מוגבלים ביותר, לעובדה זו אין משמעות גדולה. אך אם נשתמש בשני קיביטים, כשכל אחד בסופרפוזיציה של <0| ו- <1|, נקבל בעצם סופרפוזיציה של כל ארבעת האפשרויות:
כל פעולת חישוב כעת תניב סופרפוזיציה של ארבע התוצאות. באופן דומה, אם נשתמש, למשל, ב-20 קיוביטים, יהיו בתא זיכרון אחד יותר ממיליון ערכים (220=1,048,576), וכל פעולת חישוב תתבצע על כל המיליון במקביל! במבט ראשון ניראה שנמצא הפתרון לבעיות 'קשות מאד' לפיתרון, אלו שמספר החישובים בהם לנתון בגודל N הוא מסדר גודל של 2N: נכין תא זיכרון ('רגיסטר' בלע"ז) בן N קיוביטים, נכין את כל אחת מהקיוביטים במצב סופרפוזיציה של <0| ו-<1|, וכך נקבל את כל 2N הערכים האפשריים. כעת נבצע את החישוב, מסובך ככל שיהיה פעם אחת בלבד, ומכניקת הקוונטים תדאג להפעיל כל פעולה 2N פעמים. רעיון מעולה אך למרבה הצער אינו ישים, וזאת משתי סיבות: ראשית, אין שום אפשרות לחלץ את התשובה הנכונה מבין 2N הערכים האפשריים. לדוגמה: נאמר והשתמשנו ב-20 קיוביטים לתיאור בעיית הסוכן הנוסע. הרכבנו את הסופרפוזיציה המכילה יותר ממיליון ערכים (220) והפעלנו תכנית שמוצאת את הנתיב הקצר ביותר ומסמנת אותו בָּערך 1. כעת ברגיסטר התשובה ישנם מיליון ערכים, אחד מהם הוא 1 והוא מסמן את הנתיב הקצר ביותר, בעוד כל השאר הם 0. אם נמדוד כעת את הרגיסטר, הסיכוי שנקבל את התוצאה 1 הוא אחד למיליון... זאת אומרת, שאם ברצוננו להיות בטוחים שנקבל את התוצאה הנכונה (1) עליינו לחזור על החישוב ועל המדידה לפחות מיליון פעמים, ובתקווה שבאחד החישובים תעלה בגורל התוצאה הרצויה. והרי כל מטרתנו מלכתחילה היתה לצמצם את מיליון החישובים לחישוב קוונטי אחד. בכדי לתקוף מגבלה זו, האלגוריתמים הקוונטיים חייבים להכיל מנגנון המגביר את ההסתברות למציאת התשובה הנכונה מבין אוסף הערכים בסופרפוזיציה. ואכן, זהו האתגר הגדול של התכנות הקוונטי. בעייה נוספת העומדת בפני המתכנת הקוונטי היא שהאלגוריתמים האפשריים לביצוע על מחשב קוונטי מוגבלים מבחינות רבות. פעמים רבות לא ניתן להמיר תוכנית 'קלאסית' לקוונטית. הפעולות הקוונטיות, למשל, הן הפיכות. זאת אומרת שאם הפעלנו פעולה מסויימת על רגיסטר קוונטי וקיבלנו תוצאה, ניתן להפעיל כעת את היפוך הפעולה ולקבל חזרה את הערך ההתחלתי (גם אם היה סופרפוזיציה מורכבת). שער NOT עונה לדרישה הזו, אך שערי AND ו-OR אינם הפיכים: אם אנו יודעים שתוצאת חישוב של שער AND היתה 0, אין אנו יכולים לדעת אם הקלט היה (0,0), (0,1), או (1,0). למרבה המזל, קיים תחום שלם במתמטיקה העוסק בפונקציות הפיכות. אם למשל ברצוננו לבצע חישוב המתבסס על שני קיוביטים a ו-b. במחשב קלאסי יכולנו פשוט לחשב את התוצאה: x=f(a,b) מבלי לדאוג להפיכות הפונקציה f. אך במחשב קוונטי כל הפעולות חייבות להיות הפיכות, למרבה המזל הוכך שניתן להשתמש בקיוביט נוסף כדי לקבל פונקציה הפיכה. כך, במקום לחשב את התוצאה x, הפונקציה הקוונטית q תקבל שלושה קיוביטים, (a, b, c), ותפיק שלושה קיוביטים כאשר a ו-b ישארו זהים לערכם ההתחלתי, ואילו c תקבל את תוצאת החישוב. הכי פשוט להביט בדיאגרמת מלבנים של התהליך: 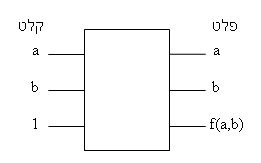
תרשים 5כך, הפלט של שער קוונטי שמחשב שער AND יהיה (0, 1, 0) ויבהיר לנו שהקלט היה (1, 1, 0) וקיוביט c הפך מ-1 ל-0. בעייה אחרת העומדת בפני המתכנת הקוונטי ידועה בשם משפט אי ההעתקה (no-cloning). כזכור, אין אפשרות למדוד בוודאות מצב קוונטי של חלקיק בודד. אך אם יש בידינו אוסף של חלקיקים שאנו יודעים שכולם במצב זהה, ניתן לבצע מספר מדידות שיגלו לנו לבסוף מה היה המצב ההתחלתי של אוסף החלקיקים. אך אם יש אפשרות לשכפל חלקיק קוונטי, אזי בהינתן חלקיק בודד נשכפלו למספר גדול כרצוננו של חלקיקים זהים, וכעת נבצע את המדידות על אוסף החלקיקים. מסתבר שהטבע לא מאפשר התחכמויות זולות שכאלו והוא מונע את היכולת לשכפל מצב של חלקיק קוונטי. המשמעות היא שמתכנת קוונטי לא יכול ליצור עותק של רגיסטר קוונטי כדי לבצע חישוב ביניים כפי שנעשה פעמים רבות במחשבים קלאסיים (גם באלגוריתם שנתתי לדוגמה, שלב 2 דורש יצירת עותק של הערך בתא X לתוך תא N). המגבלה האחרונה על מתכנת קוונטי היא שאי אפשר לבצע פקודות 'אם' (IF) על רגיסטר קוונטי. אחד הכלים העקריים בידיו של מתכנת 'קלאסי' הוא הפקודה המאפשרת למחשב לבחור לבצע סידרת פקודות אחת או אחרת בהתאם לערך של משתנה. המבנה יראה משהו כמו (הכתיב המדוייק שונה בין שפה לשפה): IF A=1 THEN אוסף פקודות כלשהו... ELSE אוסף פקודות אחר... END IF באלגוריתם שנתתי, בשלב 5 מבצעים פקודת IF. אם A הוא רגיסטר קוונטי, המחשב עצמו אמור להיכנס למצב סופרפוזיציה: בחלק אחד של הסופרפוזיציה יתבצע אוסף הפקודות הראשון, ובחלק השני של הסופרפוזיציה יתבצע אוסף הפקודות השני. אך כזכור, מחשב קוונטי הוא מחשב רגיל ('קלאסי') המשתמש ברגיסטרים קוונטיים, לכן המחשב עצמו לא יכול להיכנס למצב של סופרפוזיציה. למגבלה זו השלכות רבות משום שגם לולאות FOR משתמשות במנגנון 'אם' לצורך בדיקה אם הלולאה הסתיימה. לולאת FOR ניראית כך: FOR I=1 TO N DO אוסף פקודות... END FOR כאשר אוסף הפקודות יתבצע N פעמים, בהתאם לערכו של המשתנה N. אם N היה רגיסטר קוונטי המחשב היה צריך להיכנס לסופרפוזיציה שבה ביצע את הפקודות מספר שונה של פעמים... שער 'CNOT'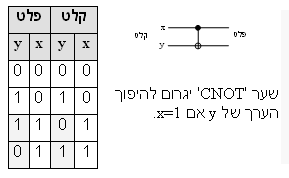
תרשים 6שתי מגבלות אלו הן חמורות ביותר, משום שכוחו וגמישותו של המחשב ביכולתו לבצע פעולות שונות בתנאים שונים, ולשם כך נדרשות פקודות IF ו-FOR. אך למרבה המזל המגבלות אינן מוחלטות ובמקרים מסויימים ניתן לעוקפן. ראשית, ניתן לבצע פקודות IF ו-FOR על משתנים שאינם קוונטיים. למשל, אם בבעיית הסוכן הנוסע ישנן N ערים, והמספר N נתון לנו כמשתנה בתכנית שאינו קוונטי, אפשר לבצע לולאות N פעמים. את המגבלה על פקודת IF ניתן לעקוף באופן חלקי אפילו לגבי משתנים קוונטיים. לשם דוגמה נביט על השער הקוונטי 'מהפך-מבוקר', Controlled-NOT או בקיצור CNOT (תרשים 6). שער זה גורם להיפוך הערך בכניסה y אם הערך בכניסה השניה, x, שווה 1. אם x שווה 0 לא יגרם שום שינוי ל-y. פעולה זו היא הפיכה ולכן יכולה לשמש כשער קוונטי, דהיינו גם x וגם y יכולים להיות ערכים קוונטיים במצב של סופרפוזיציה. אם, למשל, x היה בסופרפוזיציה של 0 ו-1 ואילו y היה במצב 1, בפלט של השער תהיה סופרפוזיציה של שני המצבים: x=1, y=0 היות ו-x גרם להיפוך הערך של y, ו-x=0, y=1 היות ו-y נותר בערכו המקורי. מסתבר שישנה משפחה שלמה של שערים קוונטיים מסוג 'מבוקר', דהיינו פעולה מסויימת מתבצעת רק בענפי הסופרפוזיציה שבהם קיים ערך מסויים. כך שבעצם במידה מסויימת ניתן לבצע פעולות מסוג IF באופן קוונטי. פעולות מבוקרות אלו לא מכסות את שלל האפשרויות שפקודת IF מאפשרת במחשב קלאסי, אך הן מאפשרות גמישות מסויימת. לאחר שלמדנו בתחילת המאמר כי את כל הפעולות הלוגיות הקלאסיות ניתן לבצע בעזרת חיבורים שונים של שער אוניברסלי אחד, הלא הוא שער ה-NAND, נשאלת השאלה האם ניתן להרכיב כל מחשב קוונטי משער אוניברסלי יסודי. חוקרים שבדקו את התחום מצאו שלתיאור כל מחשב קוונטי שהוא נדרשים שני שערים יסודיים. השער האחד פועל על צמד קיוביטים והוא מיודענו המהפך המבוקר, CNOT. השער השני הוא בעצם משפחה של שערים 'מסובבים'. נזכור שקיוביט במצב סופרפוזיציה ניראה במידה מסויימת כאילו הוא 'מסובב' מהמצב היסודי <1| (תרשים 4). פעולת הסיבוב הזו היא יותר מסובכת מהסיבוב שאנו מכירים היות וזוית הסיבוב היא מספר מרוכב, אך מכל שאר הבחינות זהו סיבוב בין שני המצבים: <0| ו-<1|. כך שמשפחת כל השערים המסובבים (השער שמסובב במעלה אחת, השער שמסובב ב-2.76 מעלות, השער שמסובב בפאי מעלות וכו' – יש אינסוף שערים כאלו) בצרוף השער CNOT[3] מאפשרים להרכיב כל מחשב קוונטי שהוא. למה טוב מחשב קוונטי?לאור המגבלות שפרוטו בסעיף הקודם, יש לצפות שלא כל אלגוריתם 'קשה מאד' לחישוב אפשר יהיה לחשב בזמן קצר במחשב קוונטי. ואכן, עד היום נמצאו רק שני אלגוריתמים לבעיות מעניינות שחישוב קוונטי מאפשר יעילות גדולה במידה ניכרת על פני מחשבים קלאסיים. אלגוריתם אחד הוא האלגוריתם של גרובר, שפותח בשנת 1996 על ידי לב גרובר והוא משמש לחיפוש מידע במסדי נתונים. אציג אותו בעזרת דוגמה: נניח שנתון לנו מסד הנתונים המכיל את מרשם התושבים של ישראל, כך שניתן לשאול אותו שאילתה Q כדוגמת: "מה מס' תעודת הזהות של אדם בעל חמישה ילדים שמספר הבית שלו שווה לשם שלו בגימטריה". בהנחה שבמרשם האוכלוסין לא מחזיקים אינדקס שיאפשר להגיע ישירות לאנשים בעלי התכונות הללו, אזי יש לחפש בכל 6,748,400 איברי מסד הנתונים עד שנמצא את האדם העונה לקריטריון. לפעמים נמצא את האדם המתאים לאחר בדיקת 100 רשומות, אך לפעמים הוא ימצא דוקא ברשומה ה-6,748,398, בממוצע נחפש במחצית הרשומות. אך אם מסד נתונים הוא קוונטי, ניתן להשתמש באלגוריתם של גרובר לצמצום מספר החיפושים. מסד נתונים קוונטי הוא מסד נתונים בו ניתן לשאול את השאלה: "האם X עונה לקריטריון C" כאשר X יכול להיות בסופרפוזיציה של מספר איברים. במקרה כזה גם התשובה תהיה בסופרפוזיציה: 0 בכל ענפי הסופרפוזיציה שבהם איברים שלא עונים לקריטריון C ו-1 בענף שמקיים את C. במקרה כזה השאילתה תהיה "האם האדם בעל מספר ת"ז X הוא בעל חמישה ילדים ומספר הבית שלו שווה לשם שלו בגימטריה", ו-X יהיה משתנה קוונטי שבו סופרפוזיציה של כל 6,748,400 מספרי תעודת הזהות. בתשובה, כאמור, נקבל 0 בכל ענפי הסופרפוזיציה, חוץ מאותם ענפים שבהם הקריטריון מתקיים. כפי שתואר בתחילת המאמר, במקרה כזה יהיה קשה מאד 'לדוג' את התוצאות הרצויות מהסופרפוזיציה, היות וההסתברות שבמדידה נקבל את התוצאה שחיפשנו היא בדיוק אותה ההסתברות כאילו בחרנו איבר אקראי ממסד הנתונים ובדקנו האם הוא עונה לקריטריון, דהינו 1/6,748,400. במקרה כזה, יש לחזור על החיפוש ועל פעולת המדידה סדר גודל של 7,000,000 פעמים כדי להיות בטוחים שבאחת המדידות נקבל את התוצאה הרצויה. כך שהחישוב הקוונטי איפשר לחפש בפעולה אחת במסד הנתונים, אך כדי לחלץ את התשובה מתוצאת החיפוש עלינו לבצע את אותו מספר הפעולות שהיינו נדרשים במקרה הקלאסי. בנקודה זו
נכנס האלגוריתם של גרובר ומתאר כיצד ניתן לנצל את תופעת ההתאבכות הקוונטית בכדי
להחליש את ההסתברות 'להגריל' בעת המדידה תוצאה שלילית ולחזק את ההסתברות לקבל
תוצאה חיובית. כך שההסתברות לתוצאה חיובית תעלה מ-1/6,748,400 לערכים גבוהים יותר.
ניתן לחזור על האלגוריתם עוד ועוד ובכל פעם ההסתברות תגדל. נמצא שלאחר
האלגוריתם השני בו חישוב קוונטי מאפשר חישוב מהיר בהרבה מהחישוב הקלאסי הוא האלגוריתם של שוֹר לפרוק מספר לגורמיו הראשוניים. מהו פרוק לגורמים? (למי שהספיק לשכוח מאז למד זאת בבית ספר יסודי) כל מספר שלם, או שהוא ראשוני או שלא. מספר ראשוני מתחלק ללא שארית רק ב-1 ובעצמו. מספר שאינו ראשוני מתחלק למספרים אחרים. מן הסתם, כל מספר בסופו של דבר מתחלק לאוסף של מספרים ראשוניים. המספר 12 למשל מתחלק ל-2 ו-6 (2x6=12), אך 6 בעצמו אינו ראשוני והוא מתחלק ל-2 ו-3. כך ש-12 מתחלק ל: 2, 2 ו-3. כדי למצוא את המחלקים של מספר בן N ספרות יש לחפש לפחות עד השורש הריבועי של אותו המספר (שאלה למחשבה: למה רק עד לשורש הריבועי?). בהנחה שהמספר הוא בינארי בן N ספרות, מדובר ב- 2N/2 חישובים. כזכור, בעיות עם מספר מעריכי של חישובים נחשבות 'קשות ביותר' לפיתרון. האלגוריתם של שור מייצר גם הוא סופרפוזיציה של ערכים אפשריים, ומשתמש בהתאבכות הקוונטית כדי להחליש את כל הערכים שאינם מחלקים ללא שארית את המספר הנבדק, כך שמדידה תמצא בהסתברות גבוהה מאד את המחלקים הראשוניים. ומה הרבותא, תאמרו, באלגוריתם שכל יכולתו מתמצית בפרוק מספר לגורמיו הראשוניים? ובכן, זו אינה "שאלת מיליון דולר", אלא שאלה של מליארדים רבים של דולרים. כל מערכות ההצפנה המשמשות בהעברות בנקאיות ובאבטחת אתרי אינטרנט משתמשות בהליך הצפנה המבוסס על עובדה פשוטה: למחשב קל מאד למצוא שני מספרים ראשוניים בני 100 ספרות ולהכפיל אותם. אך בהינתן המכפלה (בת 200 ספרות), בלתי אפשרי למצוא את שני הגורמים הראשוניים. כזכור, יש לבצע 2N/2 חישובים כדי למצוא את הגורמים הראשוניים. במקרה שלנו מדובר ב-2100 חישובים, שהם בקירוב 1030 חישובים, דהינו, מספר עשרוני בן 30 ספרות. אם כל חישוב לוקח מיליונית השנייה, תהליך הפרוק יארך כ-40,000,000,000,000,000 שנים! (נזכיר שע"פ התיאוריה הקוסמולוגית, גיל היקום הוא כ-13,000,000,000 שנים...) כך שבמצב הנתון, מציאת הגורמים הראשוניים של מספר בן 200 ספרות היא אכן בלתי סבירה. אמנם פורסם המקרה בו סטודנטים כתבו תכנה המחלקת את מטלת החישוב בין מחשבים רבים בעת שאינם עסוקים במטלות אחרות, והפיצו אותה על גבי מאות מחשבים באוניברסיטאות. באמצעות אלגוריתמים מחוכמים הם הצליחו לאחר מספר חודשים לפצח קוד בודד בן 174 ספרות. אם כך לכל צורך מעשי, קידוד על ידי מספר בן 200 ספרות הוא עמיד בפני פריצה. והנה ב-1994 פירסם פיטר שור את האלגוריתם המאפשר לפצח את הקוד בזמן סביר. לכאורה, כל תשדורת מאובטחת באינטרנט, בצבאות השונים, או בין הבנקים, בעצם ניתנת לפיצוח. אז מדוע אנו ממשיכים להשתמש באותם כלים להצפנה גם היום, 10 שנים מאוחר יותר? איפה אפשר לראות מחשב קוונטיאו, אז זהו, שקצת קשה לראות מחשב קוונטי היום. ולא בגלל גודלו. בדרך כלל מחשב קוונטי ממלא חדר מעבדה באוניברסיטה. וכאן הבעייה – עקב הקשיים העצומים בבניית מחשב קוונטי, המחשבים הקיימים היום הם רק בגדר ניסויים במעבדות אוניברסיטאיות או מכוני מחקר. כזכור, גדולתו של מחשב קוונטי היא ביכולות לבצע פעולות על רגיסטרים קוונטיים הנשמרים במצב של סופרפוזיציה. אך לא פשוט לשמור על מערכת במצב של סופרפוזיציה. כל פוטון (חלקיק אור) תועה, או מולקולה של אויר שבאה במגע עם מערכת קוונטית מהווה בעצם 'מכשיר מדידה' וגורמת ל'קריסת' מצב הסופרפוזיציה. כך שמחשב קוונטי נדרש לשתי מטלות מנוגדות: מחד, החלקיקים שמהווים את הקיוביטים חייבים להיות מבודדים לחלוטין מהסביבה כדי לשמר את מצב הסופרפוזיציה לאורך זמן. מאידך, חלק מהותי בתהליך החישוב הוא בקרה של המחשב על אותם החלקיקים והבאתם לידי פעולה הדדית בשערים הלוגיים השונים. כיום ישנן מספר טכנולוגיות נסיוניות המשמשות לבניית מחשבים קוונטיים. הרעיון המוביל הוא שימוש בתהודה מגנטית גרעינית. כקיוביטים משמשים גרעיני אטומים בתמיסה. הגרעינים באטומים הללו מתנהגים בדומה למגנטים קטנים והם יכולים להיות מאורגנים במקביל לשדה מגנטי חיצוני ('1') או בכיוון מנוגד ('0'). בעזרת פולסים של קרינה אלקטרומגנטית ניתן לשלוט בכיוון הגרעינים, 'לקרוא' את כיוונם וליצור קשר ביניהם. היתרון הוא שגרעיני אטומים מבודדים היטב מסביבתם (האלקטרונים בקליפת האטום יוצרים קשר עם הסביבה, אך הגרעין מבודד ממנה) ולכן אין צורך בבידוד מהסביבה, אך מאידך כדי לשלוט בהם ולקרוא את ערכיהם יש צורך בשדות אלקטרומגנטיים אדירים. בעייה נוספת היא שכדי להבדיל בין הקיוביטים השונים, יש צורך להשתמש במולקולות ספציפיות בהן התדרים האופיניים לאטומים רחוקים מספיק כדי שאפשר יהיה לפעול על כל אטום בנפרד (אם התדרים יהיו קרובים, נסיון לפעול על אטום אחד יפגע באטומים נוספים). נסיונות אחרים הם להשתמש בחלקיקי אור, הלא הם הפוטונים. ניתן לבצע פעולות קוונטיות רבות על פוטונים, אך הפוטונים עצמם לא יכולים להשפיע אחד על השני. כך שכדי לממש שערים קוונטיים יש להשתמש בחומרים מיוחדים שמשנים את מצבם בהתאם לפוטון שפגע בהם, וכך הפוטון השני מושפע מהחומר המתווך ומשנה את מצבו בהתאם. חומרים אלו נדירים מאד והפעולות שניתן להשיג אתם מוגבלות עדיין. יש גם קבוצות המנסות להשתמש ביונים (אטומים טעונים) השמורים ב'מלכודות יונים' מבודדים מסביבתם. בעזרת ליזרים ניתן לגרום לאלקטרונים הסובבים אטומים אלו להתרחק מהגרעין או להתקרב אליו (לעלות או לרדת ברמת האנרגיה). באמצעים אחרים ניתן 'לקרוא' את רמת האנרגיה של היונים הללו ולקבל את תוצאת החישוב. אם כך, מה מחשבים קוונטיים יודעים לעשות? ובכן, ב-1998 הוצג המחשב הקוונטי הראשון בטכנולוגית NMR והוא היה בעל שני קיוביטים. ב-1999 הוצג מחשב בעל 3 קיוביטים, ב-2000, חמישה, וב-2001 מחשב קוונטי בעל שיבעה קיוביטים מצליח בעמל רב ליישם את האלגוריתם של שור ולמצוא שהמספר 15 מתפרק ל-5 ו-3... ניראה שאנו יכולים להיות רגועים. יקח עוד זמן רב עד שמחשב קוונטי יוכל לפרוץ למאגרי המידע שעל האינטרנט או למערכות הצבא. אבל יום זה בוא יבוא. ואם לא נשכיל להכין מבעוד מועד מערכות הצפנה עמידות בפני אלגוריתמים קוונטיים, כל המערכת הכלכלית המערבית יכולה לקרוס בין ליל.
לקריאה נוספת:
[1] במאמר זה, 'קלאסי' הינו ההפך מקוונטי. מחשב קלאסי, אם כן, הוא המחשב המוכר לנו מחיי היום יום. [2] שאלה מעניינת היא כיצד אפשר להוכיח כי משהו אינו מן האפשר. אכן, שאלה טובה, אבל במאמר זה לא אוכל להראות את ההוכחה – אף על פי שהיא קצרה ואלגנטית. [3] למען הדיוק יש לציין שלא מדובר בדיוק בשער CNOT אלא במשפחת השערים דמויי CNOT אך בתוספת פאזה מרוכבת על הקיוביט שעבר היפוך. |
| Shahar Dolev שחר דולב | | | Articles מאמרים | | | Presentations מצגות | | | Downloads קבצים להורדה | | | Politics פוליטיקה | | | Fun פאן |